- 1.1 Level
- 1.2 Prerequisite knowledge
- 1.3 Suitable modules
- 1.4 Intended learning outcomes
- 2.1 Instructions
- 5.1 Game Theoretical Background
- 6.1 Results by rounds
- 6.1.1 First Round
- 6.1.2 Second Round
- 6.1.3 Third Round
- 7.1 Influences on Group Investments
- 7.2 Influences on Payments
Overview
Level
Prerequisite knowledge
Suitable modules
Microeconomics, Public Economics
Intended learning outcomes
Participants in the experiment will
- be made familiar with a simple problem of public good provision
- experience the problem of free riding and how it hinders efficient public good provision
Description of the Experiment
At the beginning of the lesson each student receives a number of identical sheets of paper, one for each round played (we conducted 3 rounds). On every page there is the same introduction and underneath a box to fill by the participants. In it each participant must choose how much to invest into a private account and how much into a public account. The total amount of investments must be equal to ten pounds. Each person in the group will receive an equal share of the money in the group investment regardless of the amount invested in the group. Every page is numbered and the first page is used for the first round out of three. The students are asked to read through the instructions and afterwards the experiment instructor/teacher will repeat the most important points.
Instructions
“You will be in a group of 10. Each of you is requested to make a decision on how to invest £10. There is a private account and a group account. For each pound invested in the private account, you will receive one pound. Each pound invested in the group account will yield 3 pounds for the group. Each person in the group will receive an equal share (one-tenth) of the money in the group account regardless of the individual contribution.
The first investment decision will be made on the decision sheet with the number 1 on top. Then, we will collect only those sheets. Ten participants will be randomly selected. They will form the group of contibuters in the first round. We will evaluate their decisions and then announce the investments made and the payoffs received. Afterwards, we will repeat this procedure with the decision sheets for the 2nd and then for the 3rd round. Thus we will play 3 rounds overall.
Out of the thirty decision sheets collected, one participant will be selected at random at the end of the lecture. He or she will be paid in cash the amount from the corresponding period. Only the name of this winner will be revealed. Everything else remains anonymous, in particular whose decision sheets have been collected in which round and how much the winner earned.
Please make your first decision now and fill it into the first decision sheet. Ensure that no-one can see your choice."
Description of the Experiment, continued
In the experiment the group of 10 people selected is only a virtual group; every student decides alone and has no opportunity to consult other students. At the end of each round 10 decision sheets are chosen randomly and their results are taken to construct one “real” group. This makes it possible to calculate the payments for the 10 different players. The results are projected onto the screen so the audience can see the results for this representative group after each round. This is important to make learning possible. The instructor should not comment on the results and thereby influence the students´ decisions in the next two rounds. For the success of the experiment it is crucial that the instructor doesn´t highlight the fact that the secure return of a private investment is obviously higher.
For a one pound group investment the player will only receive 30 pence whereas the return on a private investment is always one pound. A rational (and myopic) agent should hence only invest into the private account.
To give appropriate incentives one person will be chosen at random and paid in cash. The maximum amount someone could earn in any round is 37 Pounds, but this high amount is quite unlikely.
The box at the end of each page in which the students fill in their investment decision looks like this:

Procedure
- Distribution of the sheets to the students
- Students have 5 minutes to read the instructions
- Instructor/Teacher repeats the main information
- Participants make their decision and hand their decision sheets in
- 10 sheets are randomly chosen
- The answers of the “representative” group are filled into an Excel Spreadsheet which is projected onto a screen via a beamer (alternatively, a black or a whiteboard can used, in which case the results on the board should be carefully copied down for later class discussions.
- The sum of the group investment is calculated and then multiplied by three. This is divided by ten and is the payment each member of the group earns
- The payments of each group member are calculated as the sum of the above plus the money in the private account.
- The instructor announces the next round, which, as the last round, is played in the same fashion.
- After the third round the instructor discuss the results of the three rounds together with the students.
- At the end of the experiment one student, who is chosen by chance, receives the amount of money in cash which he has earned in one of the rounds.
Interpretation
The person who invests the lowest amount of money is the winner of the group. This result can be easily related to reality, those people who are not willing to pay for public goods and save their money reach the highest income or utility. Because some people are paying for public goods and other people can not be excluded from consuming them. The free rider makes the highest personal profit in a situation like this.
The free rider’s behaviour can be very advantageous for a handful of people but as the number of free riders increases their payments decrease. Why? Because the total sum society is willing to pay becomes smaller whilst the number of society members stays constant. This implies that people who do pay for the group are becoming worse off. They will learn this and change their behaviour and start free riding.
We are now in a situation of undersupply of public goods in a private economy where the people can decide how much they are willing to pay for the community. Obviously the sum of marginal willingness to pay for public goods is smaller than the actual demand. Thus we have an inefficient outcome which doesn´t fit the Samuelson Rule. The Samuelson Rule tells us to balance the marginal cost of public provision with the summation across households of marginal willingness to pay to reach a first best (efficient) solution.
When you compare the different rounds you can see that the number of free riders is increasing from round to round because of learning effects caused by the projection of the results from the representative group. However, the highest payment for each round is decreasing and the lowest payment is falling sharply because of a gerneal decline in contributions from round to round. That contributions are falling over time is a standard result in public good games. (Burland & Guala, 2005) Thus free riding which is rational at the micro level causes inefficiency at the macro level. All people in the group could be benefited in case that the number of free riders declines. The same outcome would result in an increase of the marginal willingness to pay of a large number of people within the group.
Students learned relatively quickly how to maximise their payment and therefore the experiment is well suited to show how free riding can cause inefficiency and influence the supply of public goods. The provided example-tables after each round have been quite inconstistent with the overall result and seem not to influence students. Because of the fact that nearly all students have been British it is not possible to see if British people free ride more than other citizens. On the whole, besides the group is consisting of hetergeneous people there is a general tendency towards lower contribution and more free-riding.
Game Theoretical Background
This experiment is set up similar to a prisoner dilemma situation. To reach the highest return everybody should cooperate and invest 10 pounds in the group. This outcome would be Pareto efficient. In a group of 10 people everybody would receive a payment of 30 pounds. However the dominant strategy is not cooperating and therefore rational players should free ride and invest all their money in private funds. In this way he/she can maximise his/her payments. But the other players will follow this strategy and the dominant strategy equilibrium would be that everybody invests nothing for the group and keeps the 10 pounds for himself. Then each player would receive only 10 pounds obviously this outcome is less for everybody. But in the long run this outcome will be reached because of learning effects of those players who invested in the group in the first rounds.
Results of the experiment
About 150 undergraduate BA and Economics students took part in the experiment in March 2006. The procedure was exactly as described above and the setup of the experiment was identical to the way described in the beginning. These are the results of the three rounds where we treated all students as one group. Answers which didn´t fit the instructions where not taken into account. Obviously the total group investment decreased constantly from the first to the second round. This means that more people decided to act as a free rider or reduced their investment for the group from round to round. Thus implies that the payment each member receives is declining also. In the third round the payment per member is only 64% of the payment in the first round.
Round 1 Round 2 Round 3 Total Group Investment 812 599 513 Payment per Member 15,6 12,1 9,99 When we have a look on the table which was showed on the blackbord after each round the results are difficult. After each round ten answer sheets have randomly been choosen and the group payments was calculated. In contrast to the overall result the group payments increased strongly from the first to the second round and thus the payments per member increased as well.
Round 1 Round 2 Round 3 Total Group Investment 138 165 81 Payment per Member 13,8 16,5 8,1 Therefore the decisions in round three have been very contrary. The value of the total group investment was halved in comparison to the second round and dropped even under the level of the overall result. Because of the controversial tables it is very hard to make any conslusions about the influence of the provided results on the decisions of the students. Burlando and Hey (1996) examined with different experiments that there is an effect on behaviour because of nationality differences. The results of this experiment do not provide an interpretation for differences in the behaviour because nearly all students have been British. To comment on this issue the same experiment must be run in other countries as well. Generally the contributions were declining and more and more students acted as free rider from round to round. This can be seen in the graph below. More and more people behaved as free rider or reduced their group investment.
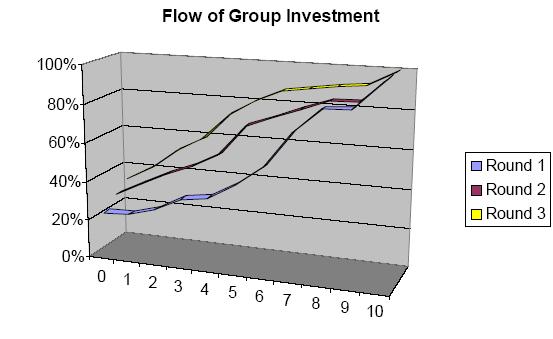
Results by rounds
First Round
How many students decided to act as a free rider in the first round? The following diagram makes it clear. About 36 students out of 156 (~23%) acted as free riders while only about 20 students (~13%) invested all their money in the group. However nearly 100 students (~65%) spent at least 5 pounds for the group. This is the reason why the overall amount of payment is so high.

Now we know how people decided to invest their 10 pounds. Leuthold (1983) pointed out that in similiar class experiments about public goods the average contribution was about 40 to 60%. This interpretation fits as well for this experiment. In the first round the average contribution to the public good was about 50% of the disposable budget. But what about the payment they got at the end of the first round? This table gives us the answer.
Highest Earning £ 25.61 Lowest Earning £ 15.61 Ratio 164% The highest earning in the first round was 25.61 pounds for all people who only invested privately. On the other side the lowest payment was 15.61 for everyone who spent all their money on the group investment. The ratio between the highest and the lowest payment is 164%, this means that the free rider receives 1.64 times the payment than the people who invested in the group. Recall that about 24% of the students earned 25.61 and about 14% earned only 15.61 pounds.
Second Round
The result in the second round shows that students are quick leaners. About 45 students out of 150 decided to be a free rider and the amount of people willing to pay at least 5 pounds for the group dropped dramatically.
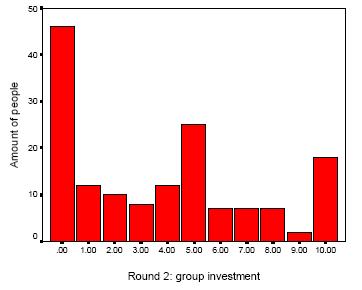
Only about 65 students (43%) invested at least 5 pounds in the group while in the round before this amount was about 100 people. You can see the enourmous change in the behaviour of the students in the graph above. Thus the total group investment dropped and the payment per member decreased from 15.61 to 12.41 pounds per player. The difference in comparison in highest and lowest earning is even larger.
Highest Earning £ 22.10 Lowest Earning]] £ 12.10 Ratio 183% The difference increased from 164% to 183% because the lowest income fell stronger than the highest payment. The more people who behave as free riders the lower the highest possible earning will be because the total payment decreases too.
Third Round
What the experiment predicts and what happened in reality is that the players will learn to reallocate their investments. This reallocation implies that more and more players are becoming free riders or are investing less into the community.
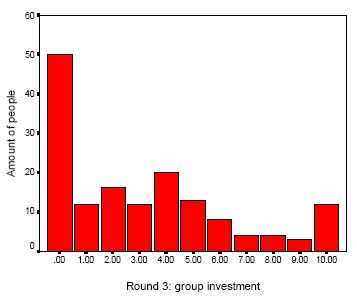
This diagram makes it clear how the students changed their minds. In the third round only about 7% invested 10 pounds in the group while one third was investing nothing. Also the percentage of players who invested at least 5 pounds in the group dropped under 30%. However this rational behaviour implied that the payments per member decreased and thus the highest and lowest earnings decreased again.
Highest Earning £ 19.99 Lowest Earning £ 9.99 Ratio 200% As we can see in the little table the difference between the two antipodes had increased again due to the strong reduction of group investments. The next diagram on the other page shows us how many people (in %) invested between 0 and 10 pounds in the last round. In the first round 23% of the players where acting as free rider, in the third round this percentage rose to one third. Only about 8% invested all their money in the group while in the beginning it was 13%. About 28% of the students invested at least 5 pounds in the group whilst in the beginning 65% invested at least 5 pounds. The majority of students did not act as a free rider but reduced their amount for the group investment dramatically over the three rounds. Not only are free riders making the system inefficient it is also the behaviour of the majority who reduce the amount of money they are willing to spend for the society.

Differences between Gender
Due to the fact that the participating students signed their answer sheets we could analyse the results in more detail. First of all we looked for differences in the decision between female and male players.
both Round 1 Round 2 Round 3 Highest Earning £ 25,61 £ 22,1 £ 19,99 Lowest Earning £ 15,61 £ 12,1 £ 9,99 Ratio 164% 183% 200% Girls Round 1 Round 2 Round 3 Highest Earning £ 26,77 £ 21,88 £ 20,01 Lowest Earning £ 16,77 £ 11,88 £ 10,01 Ratio 160% 184% 200% Boys Round 1 Round 2 Round 3 Lowest Earning £ 14,96 £ 12,13 £ 9,06 Ratio 167% 182% 200% As it is illustrated in the above table there was hardly any difference in the decision process between men and women. The prejudice that women care more about the welfare of the group does not hold true in this experiment.Contadictionary in similar public good experiments done in Isrealian Universities women seemed to free ride less than man. As well Israelian students free ride more than US American students taking part at the experiment (Kleiman & Rubinstein, 1996). However, we could not observe a differenct behaviour because of the sex of the students.
Differences between Programmes
Moreover we tested what was the influence on the student’s decisions in the experiment in course accordance to each student’s studies. We divided the students into three groups, Business Administration (BA), Economics and other studies. There were only few other students so we did not calculate the results for this group.
Business Adm. Students Round 1 Round 2 Round 3 Total Group Investment £ 217 £ 119 £ 125 Payment per Member £ 17,59 £ 11,51 £ 10,14 Highest Earning £ 27,59 £ 21,51 £ 20,14 Lowest Earning £ 17,59 £ 11,51 £ 10,14 Ratio 157% 187% 200% Economics Students Round 1 Round 2 Round 3 Total Group Investment £ 121 £ 66 £ 54 Payment per Member £ 18,15 £ 10,42 £ 8,1 Highest Earning £ 28,15 £ 20,42 £ 18,1 Lowest Earning £ 18,15 £ 10,42 £ 8,1 Ratio 157% 196% 223% We created two new societies, one for BA students and one for Economic students only. Then we calculated the results which you can see above. At a glance there are hardly any differences between the decisions made by the two groups of students. However when we look at the results in more details we can see that the Economic students learn quicker than the other students. The reduction in the group investments in round two and three are larger. As we can see in the third round there are far more free riders from the economic students than the third round than Economics students the BA students. And BA students contribute about 20% more in the group in the third round. They pay on average about £ 10 whilst the Economics students only contribute about £ 8.
Overall Round 1 Round 2 Round 3 Total Group Investment £ 812 £ 599 £ 513 Payment per Member £ 15,61 £ 12,14 £ 9,99 Highest Earning £ 25,61 £ 22,1 £ 19,99 Lowest Earning £ 15,61 £ 12,1 £ 9,99 Ratio 164% 183% 200% When we compare the results of the two groups with the overall, we can see that the groups do not really differ. About 40% of the Economics students behaved as free riders in the third round whilst overall only one third was perfectly selfish. The fact we can deduce is that Economic students realised earlier the advantages of free riding than the BA students.
Differences between Genders within Programmes
First we compared the results in BA between female and male students:
Business and Economics students:both Round 1 Round 2 Round 3 Highest Earning £ 27,59 £ 21,51 £ 20,14 Lowest Earning £ 17,59 £ 11,51 £ 10,14 Ratio 157% 187% 200% Girls Round 1 Round 2 Round 3 Highest Earning £ 28,26 £ 20,65 £ 22 Lowest Earning £ 18,26 £ 10,65 £ 13 Ratio 155% 200% 169% Boys Round 1 Round 2 Round 3 Highest Earning £ 26,5 £ 23,1 £ 17,1 Lowest Earning £ 16,5 £ 13,1 £ 7,1 Ratio 160% 176% 240% The female students did an amazing job in the second round and changed their behaviour very strongly. A lot of the female students were free riding or reducing their group investment in the second round. The difference between the highest and the lowest income was already 200%. But in the third round girls changed their mind and increased their group investments. Thus the difference between the highest and lowest payment declined. The male students behaved ambiguously in the first round, a lot of them invested a high amount in the group and a large proportion of the group was free riding. Obviously the boys didn´t change their mind as fast as the girls and the results didn´t change so much in the second round. In the third round a large proportion of boys had learnt their lesson and decided to act as free rider. Therefore the inequality between highest and lowest payment was much higher than that of the girls. Female BA students obviously put a higher value on the group investment than their male collegues and reduced the inequality between highest and lowest income. Let’s see how the economics students worked. Obviously there are strong differences between female and male students. Nevertheless it was not really easy to come up to a conclusion because only 5 female students took part in the experiment while we had 15 male students.
both Round 1 Round 2 Round 3 Highest Earning £ 28,15 £ 20,42 £ 18,1 Lowest Earning £ 18,15 £ 10,42 £ 8,1 Ratio 157% 196% 223% Girls Round 1 Round 2 Round 3 Highest Earning £ 24,4 £ 16,75 £ 14,8 Lowest Earning £ 14,4 £ 6,75 £ 10,8 Ratio 169% 248% 137% Boys Round 1 Round 2 Round 3 Highest Earning £ 29,4 £ 21,4 £ 19,2 Lowest Earning £ 19,4 £ 11,4 £ 9,2 Ratio 152% 188% 108% However boys and girls behaved quite differently to each other. While the majority of the girls acted as free rider in the second round they changed their behaviour like the female BA students in the third round. As you can see the investment in the group decreased enormously in the second round but increased again in the third round. The boys behaved like the average student in the overall results and more and more students acted as free rider from round to round.
Differences because of A-level math
We created two groups of economics and BA students who had A-levels (the 18+ qualification in the UK) in Mathematics and wanted to see if this had any influence on the results. In the second round the Economics students with A-levels in Mathematics seemed to be very quick learners and strongly reduced the amount invested in the group. However in the third round they decided to invest again more in the group and behaved differently to the overall results and the whole group of economic students.
Overall Round 1 Round 2 Round 3 Total Group Investment £ 812 £ 599 £ 513 Payment per Member £ 15,61 £ 12,14 £ 9,99 Highest Earning £ 25,61 £ 22,1 £ 19,99 Lowest Earning £ 15,61 £ 12,1 £ 9,99 Ratio 164% 183% 200% with A-level math Round 1 Round 2 Round 3 Total Group Investment £ 79 £ 43 £ 54 Payment per Member £ 16,93 £ 9,92 £ 11,57 Highest Earning £ 26,93 £ 19,92 £ 21,57 Lowest Earning £ 16,93 £ 9,92 £ 11,57 Ratio 159% 200% 186% all Round 1 Round 2 Round 3 Total Group Investment £ 121 £ 66 £ 54 Payment per Member £ 18,15 £ 10,42 £ 8,1 Highest Earning £ 28,15 £ 20,42 £ 18,1 Lowest Earning £ 18,15 £ 10,42 £ 8,1 Ratio 155% 196% 223% Business and Economics Students:
with A-level math Round 1 Round 2 Round 3 Total Group Investment £ 121 £ 64 £ 80 Payment per Member £ 18,15 £ 11,29 £ 12 Highest Earning £ 28,15 £ 21,29 £ 22 Lowest Earning £ 18,15 £ 11,29 £ 12 Ratio 155% 188% 183% without Round 1 Round 2 Round 3 Total Group Investment £ 217 £ 119 £ 125 Payment per Member £ 18,15 £ 11.52 £ 10,14 Highest Earning £ 27,59 £ 21,52 £ 20,14 Lowest Earning £ 17,59 £ 11,52 £ 10,14 Ratio 157% 187% 200% The BA students with A-levels behaved differently in comparison with the whole group of BA in the third round. They pay more in the third round then they did in the second round and contribute £ 12 on average whilst all BA students only contribute about £ 10. But in general, there are no significant differences from main importance. We can say that Alevels caused only a difference in the decision of Economics and BA students in the third round. In all other cases the results are pretty much the same with or without A-levels.
Statistical Testing of some Results
We examined the data with the help of the Software-program SPSS with the procedure of Regression with Optimal Scaling.
Influences on Group Investments
First we treated the dependent variables seperately (group investment 1, group investment 2, group investment 3) and we tried to identify which of the independent variables (gender, grades, and course) would have the biggest effect on the dependent variables. According to the Importance and the Beta values we can see which of the independent variables has more influence on the dependent variable (group investment 1). GCSE (Marks) with Importance=0.792 seems to have the biggest effect on group investment in round one.
Group Investment 1 Importance Beta Gender 0.130 0.061 Programme 0.078 -0.081 GCSE 0.792 0.182 In round two group investments are also strongly influenced by GCSE. With Importance= 0.616 the GCSE seems to have the major effect on the investments from the three independent variables.
Group Investment 2 Importance Beta Gender 0.101 -0.077 Programme 0.283 -0.114 GCSE 0.616 0.159 In round three we can observe that the results are totally different to the two previous rounds. The independent variable (gender) seems to have the biggest influence on the group investment and the marks (GSCE), which had been in the previous rounds more important than the other independent variables, have only a very low importance=0.190.
Group Investment 3 Importance Beta Gender 0.730 -0.257 Programme 0.080 -0.115 GCSE 0.190 0.149 In these three cases, which we have examined, the adjusted R square value is always close to zero. This implies that the results of the three regressions are not very reliable and we think that the impact of the independent variables on the dependent variables is relatively low. In other words, the kind of gender, programmes and the marks does not significantly influence the decisions in the experiment. We tried to find regressions which have significant results and therefore we treated the group investment in round three as the dependent variable and the group investments in previous rounds as independent variables. The adjusted R square value is 0.39 and much higher than in the regressions before, hence the result is more reliable. According to the importance values, the group investment in the second round has a strong influence on the group investment decisions in round three. The importance value is 0.8625 and the beta factor is 0.5701. Obviously the investment decisions in the second round are more important for the decisions in the third round than the investment decisions in
Multiple R R Square Adjusted R Square 0.658 0.4335 0.3912 Dependent Variable: Group Investment 3 Predictors: Group Investment 1 Group Investment 2 the first round. However this can be also the case because of similar decisions in round two and three which are linked to the learning process.
Group Investment 1 0.1735 0.2048 Group Investment 2 0.8265 0.5701 Dependent Variable: Group Investment 3 We also made a regression to predict the group investment in round two with the investment decision of round one. This linear regression shows very low R Square and Beta values and thus shows only a low statistically significance for a strong influence of the decision of round one on the decision in the next round.
Importance Beta Group Investment 1 .250 .253 Dependent Variable: Group Investment 1 Influences on Payments
We also carried out a regression where we took as the dependent variable the payments in round three and as independent variables the payments in the two rounds before. Again the adjusted R square value is 0.337 and shows us that not only these two regressors have an impact on the outcome in round three.
Multiple R R Square Adjusted R Square 0.6033 0.364 0.337 Dependent Variable: Payment 3 Predictors: Payment 1 Payment 2 Importance Beta Payment 1 0.4327 0.3464 Payment 2 0.4452 0.4110 Dependent Variable: Payment 3 Payments in round one and two, seem to have almost the same affect on the payments in round three. However the payments of the previous rounds have an indirect influence on
Multiple R R Square Adjusted R Square .253 .064 0.3912 Dependent Variable: Group Investment 2 Predictors: Group Investment 1 the payments of the third round because the investment decisions are dependent on the payments.
Conclusion
The experiment shows an easy way to test how theoretical assumptions in a lecture. The results represent pretty much the theoretical hypothesis, that people will tend to behave as free riders in a environment of private supply of public goods. The detailed analysis of the results showed that students are learning quickly, and free riders students are increasing. In the end about a third of the players acted as free riders. Obvious differences did not occurre because of gender and the quality of marks. Economic students were slightly outperforming BA students in the third round. However, the differences are very small. In the analysis with regressions we could see that previous group investment decisions have an influence on later decisions. The same applies for payments but this was intuitive. For further ways of discussing the results with students we refer to Holt & Laury and their paper about classroom experiments.
Literature
- Burlando, Roberto & Guala Francesco (2005): Heterogeneous Agents in Public Good Experiments. Experimental Economics. Vol. 8 pp. 35- 54.
- Burlando, Roberto & Hey John D. (1997): Do Anglo-Saxons free-ride more? Journal of Public Economics. Vol. 64 pp. 41 – 60.
- Holt, Charles A. & Laury Susan K. (1997): Classroom Games: Voluntary Provision of a Public Good. The Journal of Economic Perspectives. Vol. 11 pp. 209 – 215.
- Leuthold, Jane H (1993): A Free Rider Experiment for the Large Class. The Journal of Economic Education. Vol 24. pp. 353 –
External links
- An Online Public Good Game (1 st game in the list).